Quantum Computing Made Easy: Bits and Qubits (SERIES 1)

Oleh: Togar A. Napitupulu

NB. Beberapa notasi dan persamaan matematik pada artikel ini bisa dibaca lebih baik dengan format pdf pada link ini: https://mmsi.binus.ac.id/files/2020/09/SERIES-1-Quantum-Computing-Made-Easy-Bits-and-Qubits-Togar-Alam-Napitupulu.pdf

Quantum computing merupakan topik yang mendapat perhatian luas dikalangan ilmuwan computer belakangan ini.  Kalau komputer klasik (computer yang saat ini umumnya diggunakan) didasarkan pada binary digit (bits), maka quantum computing didasarkan pada quantum bits (Qubits).  Apa yang istimewa dengan quantum computing dibandingkan dengan komputer klassik?

Pertama, quantum computer memiliki kemampuan yang jauh lebih besar dibanding computer klssik baik dari segi daya simpan (storage) maupun dari segi kecepatan.  Dari segi kepatan misalnya, time complexity untuk faktorisasi bilangan bulat yang cukup besar antara algoritma yang tercanggih computer kalssik, yaitu Number Field Sieve dibanding dengan algoritma Quantum Factorization yang dikembangkan oleh Shor, adalah Exp(1.9 log(n^1/3)*log(log(2))^2/3  lawan Log (n³).  Dengan perbedaan yang cukup jauh ini maka encripsi asimetrik yang saat ini didasarkan atas algoritma Filed Sieve akan tidak berguna dengan kehadiran algoritma Shor pada quantum computer.

Dari sudut storage, perhatikan perbandingan kapasitas storage klasik dan quantum pada table berikut:

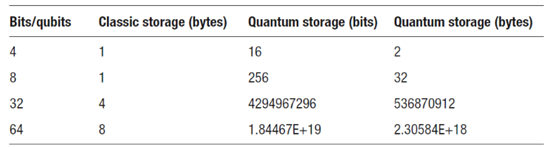
Dari table di atas terlihat kemampuan daya simpan yang sangat besar dari qubit secara simultan dengan loncatan yang sangat tinggi dari 32-Qubit ke 64-Qubit dibandingkan dengan bits dari komputer klassik. Ini akan berdampak pada berbagai bidang mulai dari searching, simulasi, optimisasi, medicine, genetic engineering, dan artificial intelligence yang selama ini tidak bisa dilakukan dengan komputer klasik, menjadi hal yang mudah dengan quantum computer. Salah satu yang mungkin menakjubkan adalah seperti pada rujukan ini : “The Mermin-Peres Magic Square is an example of quantum pseudo-telepathy or the ability of players to almost read each other’s minds achieving outcomes only possible if they communicate during the game.”

Kedua, yang sangat penting adalah, bahwa ukuran transistor saat ini, yang merupakan komponen utama computer, adalah 14 nanometer (14×10^-9 meter) yang sangat dekat dengan ukuran molekul sebesar 5 nanometer. Apabila diperkecil lagi dibawah 5 nanometer, maka akan terjadi atau muncul sifat quantum mechanics di mana transistor tidak bisa lagi menahan elektron atau photon sehingga tidak bisa lagi membedakan 0 dan 1 (masalah tunneling pada quantum mechanics). Ini berarti, kemampuan computer kasik saat ini sudah pada limitnya. Disisi lain, justru sifat tunneling inilah yang dimanfaatkan dalam quantum computing, sehingga kedepan, tidak ada jalan lain untuk meningkatkan kemampuan storage computer saat ini kecuali dengan quantum computer.

Saat ini IBM telah membuat protipe quantum computer rig (IBM Q Experience) yang tersedia atau dapat diakses melalui cloud bukan hanya bagi para peneliti tapi juga setiap individu yang tetarik dibidang quntum computing.  Oleh karena itu sudah saatnya bagi setiap mahasiswa computer untuk memulai mempelajari quantum computing ini karena dalam waktu yang tidak terlalu lama lagi semua komuter akan bebasis quantum atau paling tidak dapat diakses lewat cloud. Data center misalnya akan segera berbasis quantum computing melalui cloud.

Tulisan ini merupakan tulisan yang terdiri dari empat seri. Seri pertama merupakan pengntar dan membahas Bits vs Qubits; seri kedua membahas matematika dari Qubits; seri ketiga membahas implementasi dan representasi Qubits dalam hardware; dan seri terakhir, keempat, membahas bagaimana memrogram Quantum Computing dengan menggunakan computer IBM Q-Experience melalui cloud.

Bits

Komputasi pada prinsipnya adalah merupakan system yang memproses input dan menghasilkan output sebagai hasil akhir dari proses itu.  Pada computer klasik dengan arsitektur Von Newmann, maka input merupakan rangkaian angka nol dan satu (0 dan 1) (binary digits, hence the name “bits”) dan outputnya juga merupakan rangkaian angka nol atau satu.  Namun demikian, dalam kehidupan sehari-hari, kita tidak menggunakan bilangan biner (bilanngan berbasis 2), tapi menggunakan bilangan decimal (bilangan barbasis 10), maka bilangan decimal diubah dulu de dalam bilangan biner baru diolah; demikian pula dengan output dari system komputasi itu yang merupakan bilangan biner akan diubah dulu kembali ke bilangan decimal baru disajikan kepada pengguna. Sebagai contoh, angka 29 dalam decimal atau basis 10 dapat ditulis dalam bentuk seperti dibawah ini:

29₁₀ = 2*10¹ + 9*10⁰

Dalam basis 2 atau biner, angka 29 ditulis dengan 11101₂ (catatan, angka indeks menunjukkan basis). Padanan biner dari angka 29₁₀ didapatkan dengan membagi bilangnan itu dengan 2, lalu kemudian hasilnya dibagi lagi dengan 2. Apabila dalam proses pembagian ada sisa maka pasang angka 1 sebagai koefisien dari basis mulai dari 2⁰ pada posisi paling kanan, dan demikian selanjutnya.  Sebaliknya, bila tidak ada sisa, maka kefisiennya adalah 0, seperti pada hasil berikut ini:

11101₂ = 1*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 29₁₀

Selanjutnya, dapat ditunjukkan bahwa operasi matematika yang dalam system bilangan berbasis decimal dapat dilakukan dengan system bilangan berbasis biner. Tentu hasil pengolahan itu nantinya akan dikonversi lagi menjadi decimal.

Data dan pengolahan berikutnya yang kita hadapi dalam dunia nyata adalah pengolahan logika dimana hasilnya adalah benar atau salah (true or false), misalnya system aljabar (Boolean algebra) yang elemennya adalah true dan false tadi, tentu dengan semua operator-operator yang didefinisikan berlaku untuk system itu, bersama dengan aksioma dan dalil-dalil-nya. Dapat kita lihat bahwa ini sejalan dengan system biner dengan bits di mana true equivalent dengan bit 1 dan false equvalent dengan bit 0; dan ini pula yang menjadi dasar penerjemahan ke dalam hardware dalam bentuk gates yang akan dibahas pada seri 3 dari rangkaian tulisan ini.

Kta tahu bahwa banyak juga data sebagai input maupun output ke dan dari system komputasi klassik yang bukan numerik.  Sebagai contoh text yang terdiri dari alphanumeric, images, audio, simbol-simbol, dll., yang tentu dengan operator masing-masing. Ini pun diolah dengan representasi baku dalam bits. Sebagai contoh, utuk characters alphanumeric maupun symbol direpresentasikan dengan bits yang baku dalam ASCII.

Berikut ini akan dibahas Qubits yang murupakan unit data terkecil dalam Quantum Computing.

Qubits

Bit seperti diuraikan di atas adalah 0 atau 1. Ia dapat diwakili oleh dua keadaan yang eksklusif, seperti on dan off dari listrik – mutually exclusive states.  Bit sebelum diobservasi atau sebalum diukur atau sebelum dilakukan experimentasi (yaitu sebelum ditekan tombol on atau off-nya) pilihannya selalu sama, yaitu kalau sebelumnya 0 sesudah diukur juga ya 0; sebaliknya bila sebelum diukur 1, maka setelah diukur atau diobservasi juga 1.  Qubit, berbeda, yaitu sebelum diukur keadaanya bisa banyak kemungkinan; dan kalau sudah diukur atau dilakukan experimentasi, maka keadaannya (state-nya) hanya ada dua kemungkinan yaitu 0 atau 1. Kenapa seperti itu, ini ada kaitannya dengan representasi dari qubit, yaitu electron atau photon (partikel cahaya). Mengenai ini akan dibahas pada seri 3.

Untuk saat ini cukup kita fahami dulu bahwa qubit adalah sebagai unit vector kolom. Unit vector adalah vector dengan norm-nya sama dengan 1. Catatan, norm adalah akar dari penjumlahan kuadrat semua elemen dalam vector tersebut.  Dalam aljabar linear, vector diberi simbol dengan huruf tebal; kalau underscore makai ia adalah vector baris, sedang kalau tidak pake underscore ia adalah vector kolom. Contoh, v = (1 0 1), adalah row vector dengan tiga elemen yaitu 1, 0, dan 1. Di sisi lain, Eq 1 adalah vector kolom. Ia adalah unit vector (=3-Qubit) karena √(1^2+0^2+1^2 ) = 1.  Namun demikian, dalam tulisan ini kita akan menggunakan notasi baku untuk quantum yaitu dengan menggunakan Dirac (dari ahli quantum computing Paul Dirac), yaitu |1 0 1˃ atau Ket. (sedangkan row vector disebut Bra dengan symbol ˂1 0 1|).

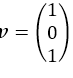( Eq 1)

Untuk lebih menyederhanakan pembahasan tanpa menghilangkan makna, maka kita akan menggunakan 2-Qubit, yaitu unit vector kolom berdimensi dua. Karena kita akan juga mengukur vector tersebut, maka arahnya juga perlu ditentukan. Arah dari vector tersebut akan ditentukan oleh basis yang orthonormal. Mialnya basisnya adalah (|1 0˃, |0 1˃) = (|b₀˃, |b₁˃), yaitu basis yang sama dengan sitem salib sumbu X dan Y yang kita semua familiar. Oleh karena itu sekarang, setiap 2-qubit v dapat ditulis sebagai kombinasi linear dari basis tadi, dalam bahasa quantum disebut superposition, sebagai berikut: d₀ |b₀˃ + d₁ |b₁˃ dimana kuadrat dari   dan merupakan peluang yang apabila qubit tersebut diobservasi atau diukur atau delakukan experimentasi, menjadi ket b₀ atau ket b₁.

Oleh karena itu, sebelum diobservasi, maka ada takterhingga 2-qubits yang merupakan kombinasi linear dari basis tersebut, yaitu semua titik atau vector yang berada disepanjang lingkaran dengan pusat pada (0, 0) pada sistim salib sumbu X dan Y (lihat Gambar 1 di bawah), tergantung d₀ dan d1.  Namun demikian, setelah dilakukan pengukuran, maka akan menjadi ket b₀ atau ket b₁ dengan peluang masing-masing   dan .  Juga kita akan mengaitkan ket b₀ dengan bit 0 dan ket b₁ dengan bit 1.  Dengan demikian, setelah dilakukan pengukuran atau experimentation, maka qubit akan menjadi bit.

Semua sytem, baik yang berkatitan dengan number system, dll., yang berlaku di system bit, tetap berlaku untuk qubit. Hanya dalam implementasinya dengan hardware, yaitu gates yang digunaan dan menggunakan cahaya (photon) sebagai sumbernya, maka berbeda dengan gates yang digunakan pada computer klassik, dan sudah barang tentu algoritma juga to some extend menjadi berubah.  Topik ini akan di bahas pada seri-seri berikutnya.

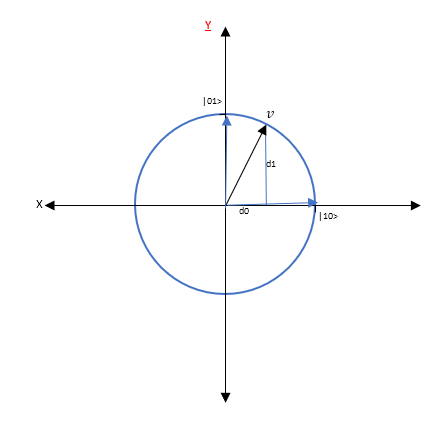
Gambar 1. 2-Qubit v dalam lingkaran dengan radius 1